728x90
반응형
문제 출처 : https://www.acmicpc.net/problem/2143
2143번: 두 배열의 합
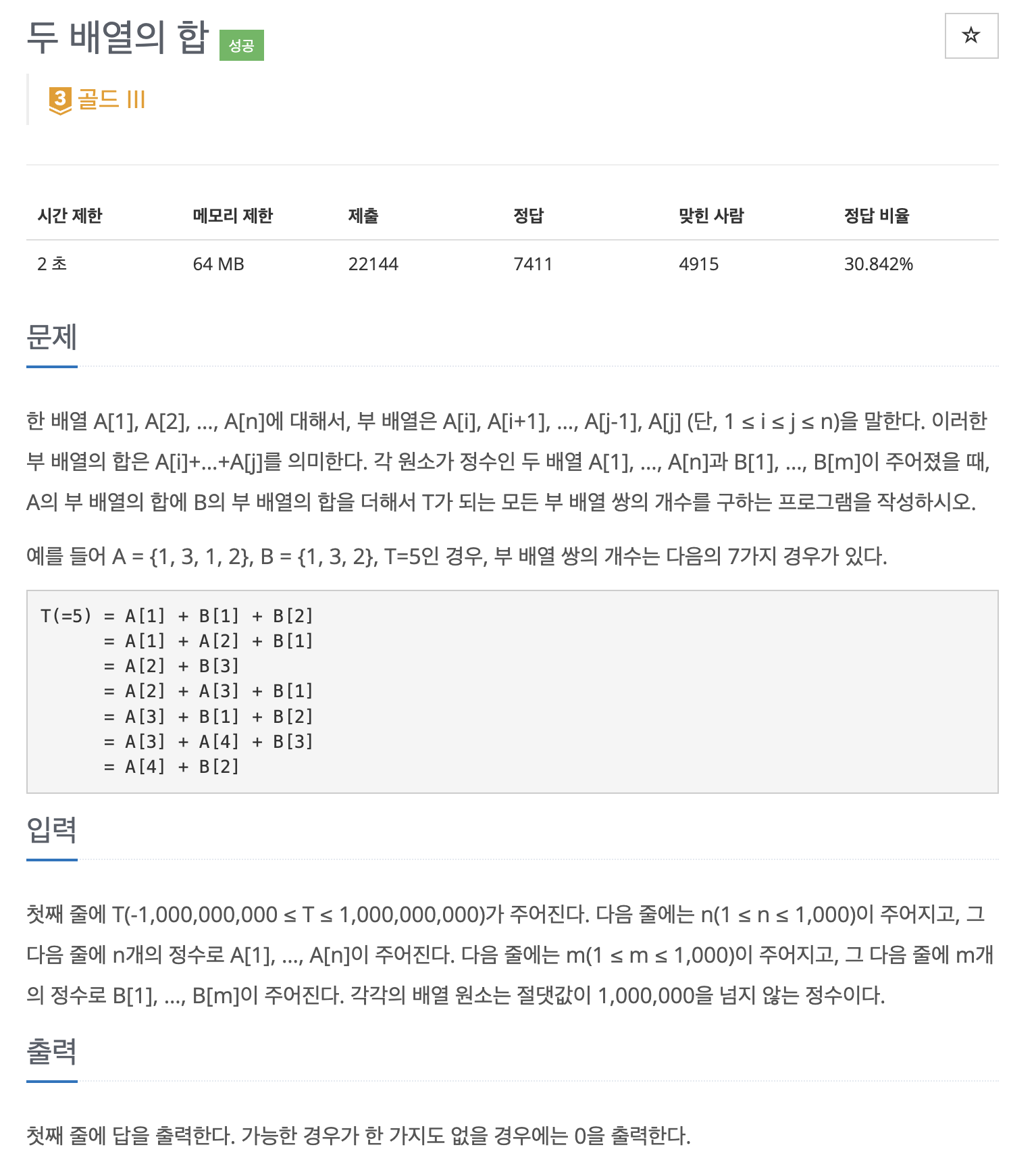
첫째 줄에 T(-1,000,000,000 ≤ T ≤ 1,000,000,000)가 주어진다. 다음 줄에는 n(1 ≤ n ≤ 1,000)이 주어지고, 그 다음 줄에 n개의 정수로 A[1], …, A[n]이 주어진다. 다음 줄에는 m(1 ≤ m ≤ 1,000)이 주어지고, 그
www.acmicpc.net
풀이
어떻게 이분탐색을 돌려야할지 고민이 되는 문제이다.
중요한 부분은, A와 B의 누적합을 미리 저장해두는 것이다.
누적 합
A, B 배열에서 모든 부 배열의 누적합을 저장한다.
vector<int> aSum, bSum;
for (int i = 0; i < N; i++) {
int sum = A[i];
aSum.push_back(sum);
for (int j = i + 1; j < N; j++) {
sum += A[j];
aSum.push_back(sum);
}
}
... b도 반복이렇게 되면, aSum, bSum에 각각 부 배열의 누적합들이 저장될 것이다.
lower_bound, upper_bound
부 배열의 쌍을 구하는 것이 정답이다. 즉 aSum의 원소와 bSum의 원소를 더했을때 T가 나오면 된다.
따라서 T - aSum의 원소 = bSum 원소 이므로, T - aSum에 해당하는 bSum의 개수를 구해주면 된다.
그렇다면 bSum의 개수는 어떻게 구할까?
바로 lower_bound, upper_bound를 활용한다.
lower_bound는 배열에서 범위 내의 원소들 중 value값 보다 크거나 같은 첫 번째 원소의 주소를 리턴
upper_bound는 배열에서 처음으로 value값을 초과하는 원소의 주소를 리턴
즉, 해당 숫자의 시작과 끝 주소를 알 수 있다.
sort(bSum.begin(), bSum.end());
long long ans = 0;
for (int i = 0; i < aSum.size(); i++) {
int target = T - aSum[i];
// 타겟과 같은 수들 개수 (hi - lo)
int lo = lower_bound(bSum.begin(), bSum.end(), target) - bSum.begin();
int hi = upper_bound(bSum.begin(), bSum.end(), target) - bSum.begin();
ans += (hi - lo);
}lo부터 hi까지 해당 수이므로 hi - lo를 더해준다.
코드
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int T, N, M;
int A[1001], B[1001];
int main(void){
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
cin >> T >> N;
for (int i = 0; i < N; i++)
cin >> A[i];
cin >> M;
for (int i = 0; i < M; i++)
cin >> B[i];
vector<int> aSum, bSum;
for (int i = 0; i < N; i++) {
int sum = A[i];
aSum.push_back(sum);
for (int j = i + 1; j < N; j++) {
sum += A[j];
aSum.push_back(sum);
}
}
for (int i = 0; i < M; i++) {
int sum = B[i];
bSum.push_back(sum);
for (int j = i + 1; j < M; j++) {
sum += B[j];
bSum.push_back(sum);
}
}
sort(bSum.begin(), bSum.end());
long long ans = 0;
for (int i = 0; i < aSum.size(); i++) {
int target = T - aSum[i];
// 타겟과 같은 수들 개수 (hi - lo)
int lo = lower_bound(bSum.begin(), bSum.end(), target) - bSum.begin();
int hi = upper_bound(bSum.begin(), bSum.end(), target) - bSum.begin();
ans += (hi - lo);
}
cout << ans;
return 0;
}728x90
반응형
'Tech > Algorithm' 카테고리의 다른 글
| [BOJ] 백준 6118 숨바꼭질 c++ (bfs) (0) | 2023.05.29 |
|---|---|
| [프로그래머스] 네트워크 c++ java (dfs) Level3 (0) | 2023.05.05 |
| [BOJ] 백준 13023 ABCDE c++ (DFS, 백트래킹) (0) | 2023.03.26 |
| [BOJ] 백준 17404 RGB거리 2 c++ (dp) (0) | 2023.03.23 |
| [BOJ] 백준 17144 팰린드롬? c++ (dp) (0) | 2023.03.21 |